Can you randomly reorder an array in `O(n)`? - Fisher-Yates Modern Shuffle algorithm

This question is similar to “shuffle a deck of cards” or “randomize a given array”, here shuffle means that every permutation of array element should be equally likely.

We can solve this problem in various ways.

Solution 1

1. Generate a random value for each item in array.
2. Use these random values as keys to sort the array, in ascending or descending order.
3. Return the array.

we have a shuffled array! Random keys will esure that each time we run the algorithm we get a new configuration of elements inside the array. Sounds cool!!

Time and Space complexity

We’d be needing O(n) extra space to store n random values which we will be using as keys in order to sort the array.

To sort the array we can use any sorting algorithm, let’s assume we’ll be using Quicksort this time, time complexity for Quicksort is O(n log(n)) and space complexity is O(log(n)).
Assuming it takes O(1) time to generate each random number.

Space complexity for entire solution = O(n) + O(log(n)) ≡ O(n)

Time complexity for entire solution = O(n) + O(n log(n)) ≡ O(n log(n))

Time complexity is not quite what we were looking for, let’s try a different solution.

Solution 2

1. Randomly select one of the “unshuffled” items.
2. Swap the selected item with the last item in the collection that has not been selected.
3. Repeat until there are no remaining “unshuffled” items left.

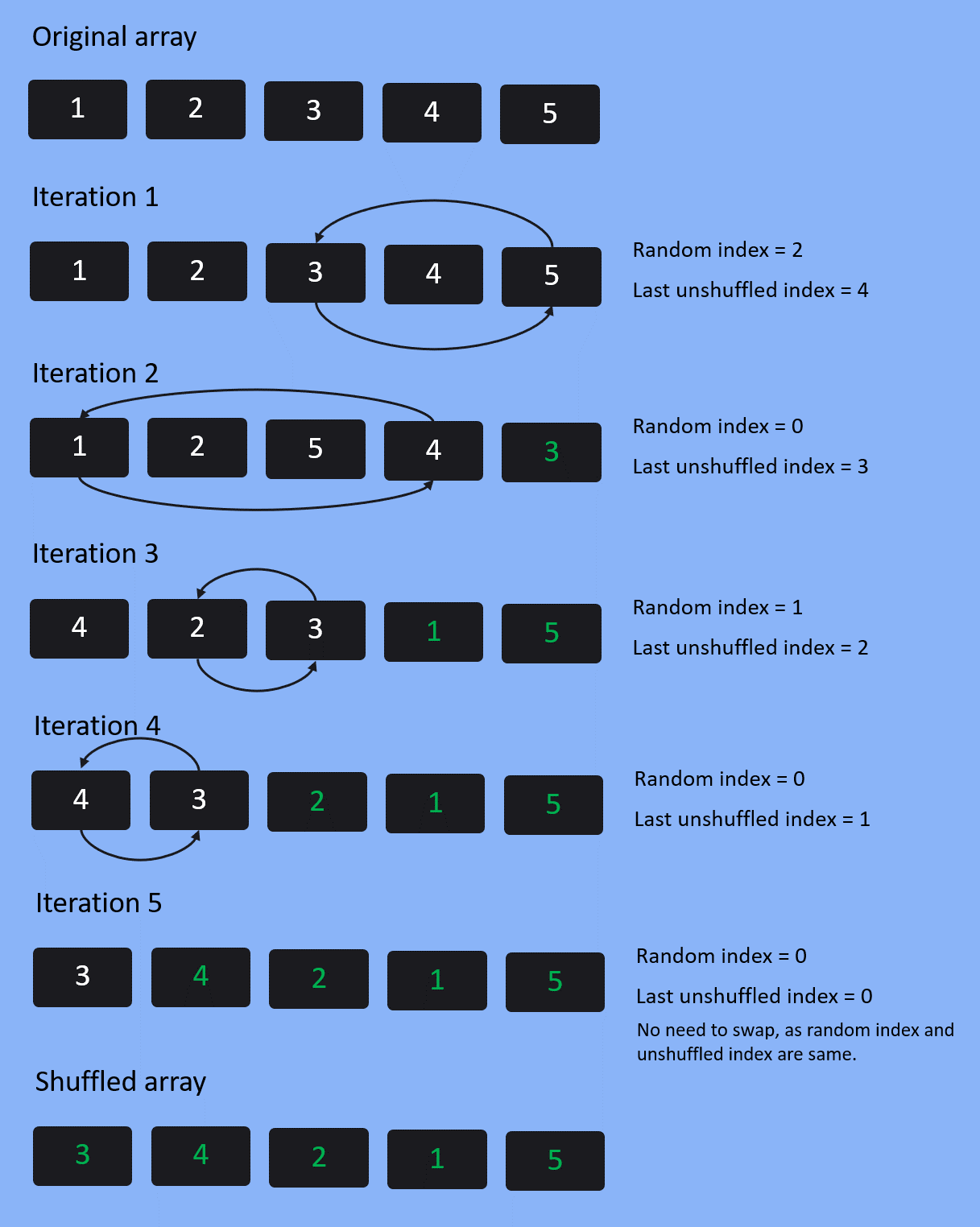
This algorithm is also known as Fisher-Yates Modern Shuffle algorithm.

Time and Space complexity

We are going to do in-place swapping which requires constant O(1) extra space.
We are iterating the array only once so time required to traverse the entire array having n elements would be O(n). Assuming it takes O(1) time to generate each random number.

Space complexity for entire solution = O(1)

Time complexity for entire solution = O(n) + O(n) ≡ O(n)

Awesome, we reordered/shuffled an array in O(n) time!

Implementation (JavaScript)

1
2
3
4
5
6
7
8
9
10

function shuffle(arr){
    var index = arr.length;
    while(--index>=1){
        var swapIndex = Math.floor(Math.random()*(index+1));
        var swapWith = arr[swapIndex];
        arr[swapIndex] = arr[index];
        arr[index] = swapWith;
    }
    return arr;
}