Disjoint Set, also know as Union Find is a data stucture that tracks a Set of elements partitioned into number of disjoint subsets.
It offers near constant time operations to add new sets, merge existing sets and to find whether items are in the same set or not, disjoint sets can be used to detect cycle in a non directed graphs, Kruskal’s algorithm uses disjoint sets to find minimum spanning tree.
Operations
Disjoint set allows following 3 operations.
- Make Set
- Find
- Union
Make Set
Make Set operation creates a new set having a new element with unique id, rank and a parent pointer pointing to itself, parent pointer pointing to itself indicates that the element belongs to its own set.
For given a graph G we will have 4 disjoint sets S1, S2, S3, S4 after performing Make Set operation.
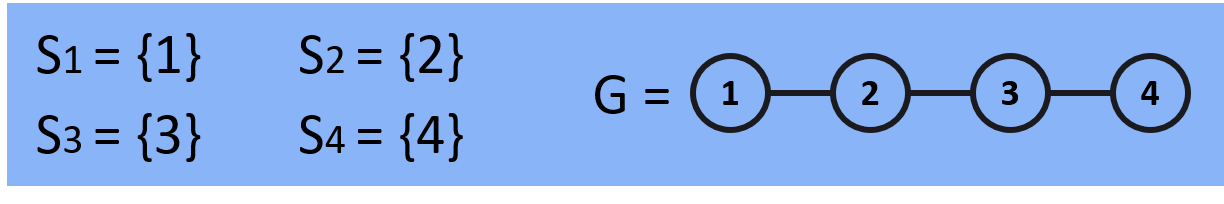
Find
Find operation on a node gives the set to which that node belongs to, It does so by following the chain of parent pointers until it reaches to a node whose parent is itself.
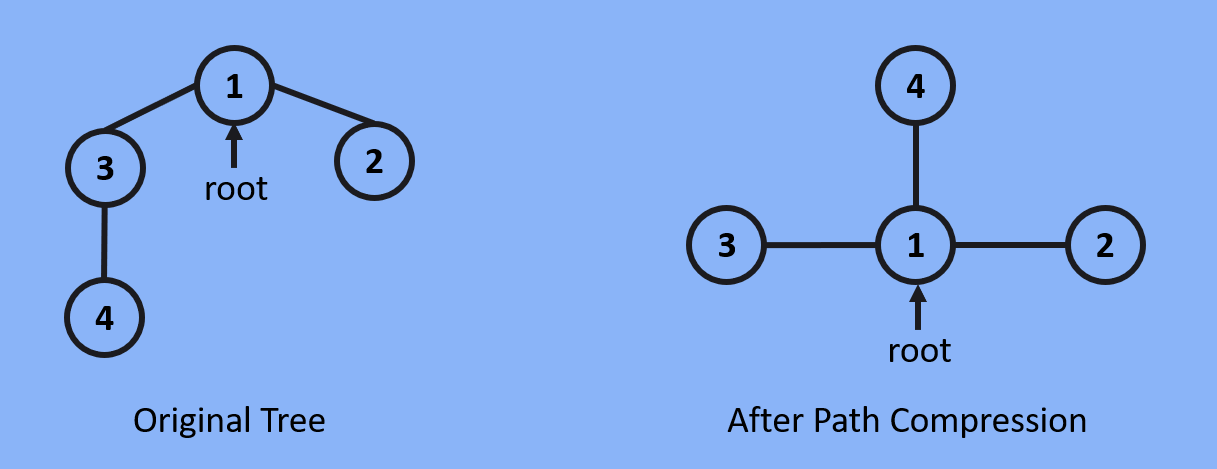
Finding root node can be expensive sometimes, because of long chain of parent nodes, to reduce the lookup time we need smaller paths between node in question and root node, using path compression technique we can reduce lookup time.
Path compression
When Find is applied on a node, path compression flattens the structure of the tree by making every node point to root node, which makes lookup chain only 1 level deep making root lookup time nearly constant. Path compression technique is possible because every node on the way to root node belongs to the same set.
Union
Union(A,B) uses Find to determine root node of A and B, if those two are distinct nodes then it combines those nodes by pointing root node of one to root node of other. if we don’t take care of which node points to which other node then the height of the tree could reach O(n) causing lookup time to surge by O(n).
To prevent such issue we perform Union by rank or Union by size.
Union by rank
Union by rank always attaches the root of shorter tree to the root of taller tree, in such case resulting tree will not be any taller than the original unless both tree were of same height, in that case resulting tree will be taller by one node.
To implement this approach each node is associated with a rank, initially a set has one element and a rank of zero, if two sets are unioned and have same ranks then the resulting set will have rank one larger, otherwise if they have different ranks then the resulting set will have the rank which is higher of two.
Union by size
Union by size attaches the root of the tree having fewer node to the root of the tree having more nodes.
Time complexity
Using both path compression, splitting, or halving and union by rank or size ensures that the amortized time per operation is only O(α(n)) where α(n) < 5 for any value of n, so the disjoint-set operations take place in essentially constant time.